
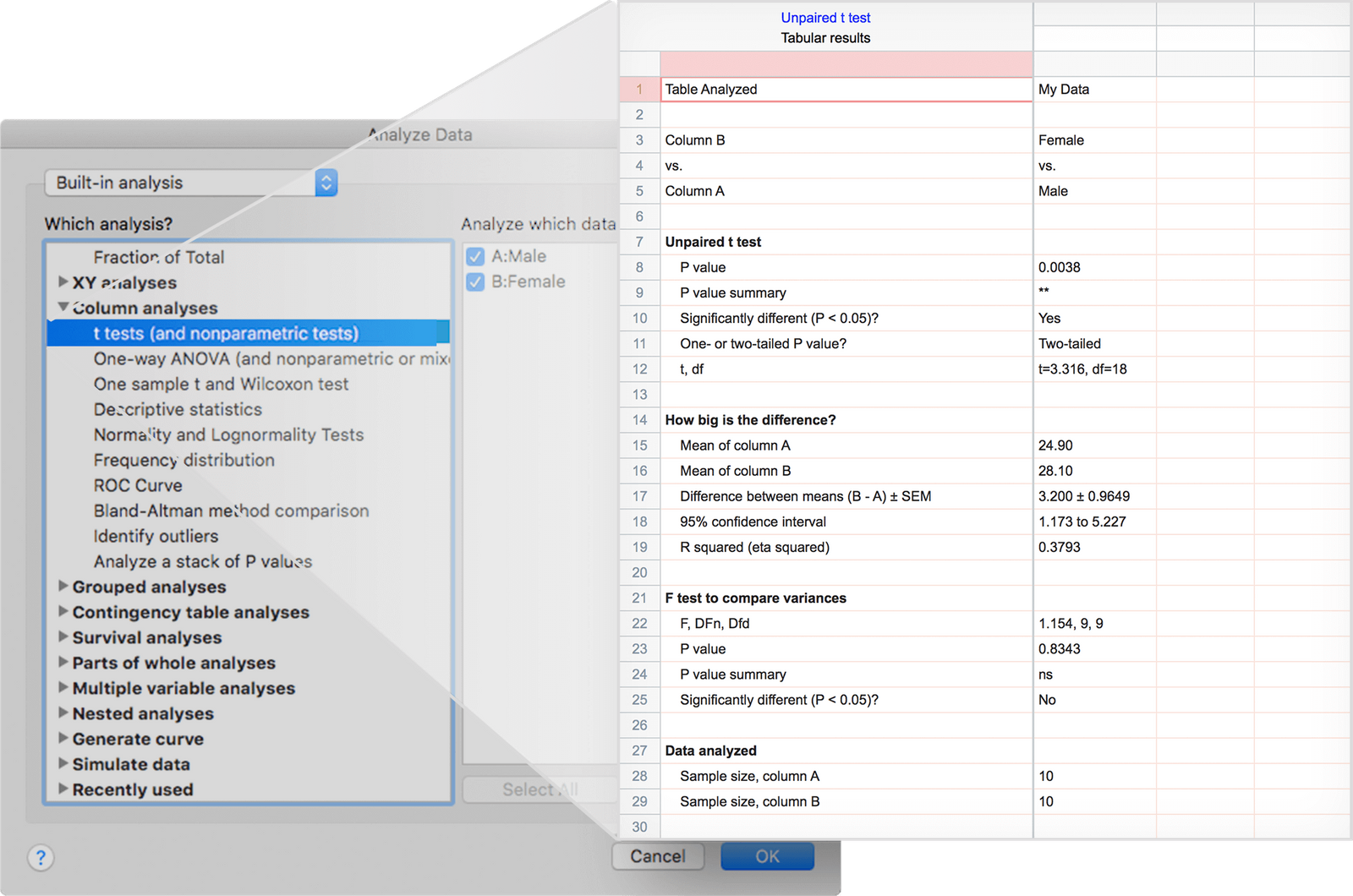
If you wanted to be fancier, you could put all the data into a two-way ANOVA, where genotype is one factor, and experiment is the other. I suspect that reporting three consistent experiments will be more informative than trying to combine all the analysis into one pooled result. Then you can report the results of all three experiments (confidence intervals and perhaps p values) and look for consistency. I'd be inclined to analyze each of your three experiments separately, with an unpaired t test or nonparametric Mann-Whitney test. My question: how can I analyse these data using GraphPad Prism? Or, alternatively: does the quoted description fit my case?įrom your description, I don't think you've really done an experiment where a repeated measures analysis (or the alternatives Frank mentioned) are appropriate.

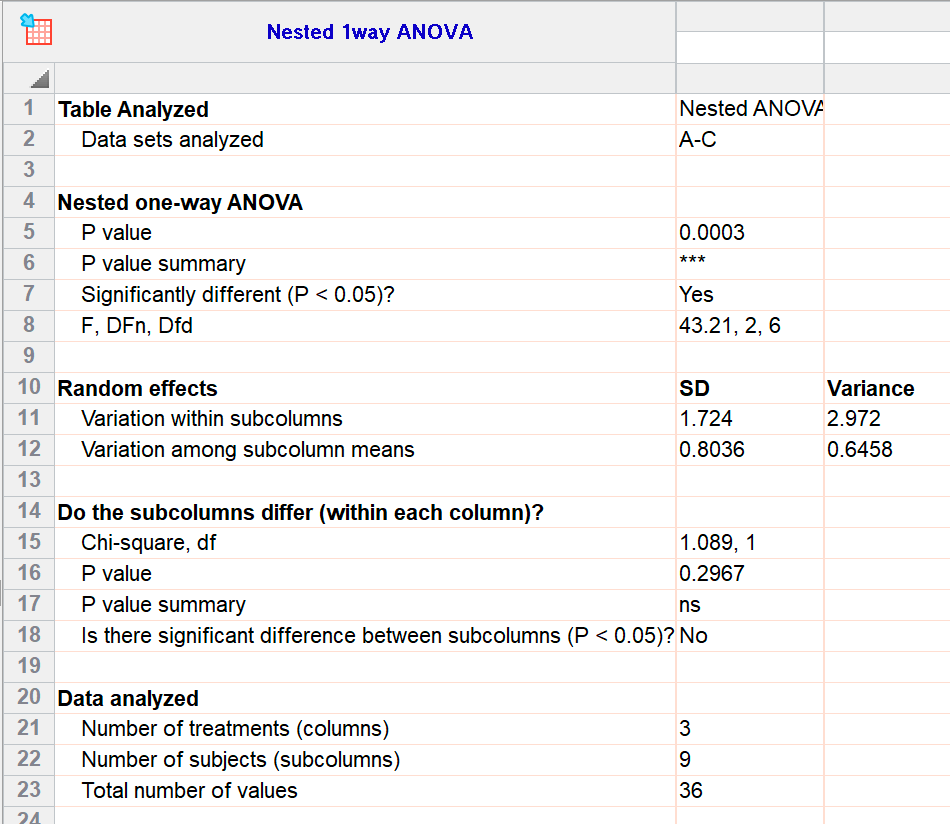
Prism always uses the term repeated measures, so you should choose repeated measures analyses when your experiment follows a randomized block design. Randomized block data are analyzed identically to repeated-measures data. The value at row 1, column A, Y1 (23) and the value at row 1, column B, Y1 (28) came from the same experiment (same cell passage, same reagents). All the Y1 data came from one experiment, and all the Y2 data came from another experiment performed a month later. For example, imagine that the three rows were three different cell lines. The term randomized-block describes these kinds of experiments. Some experiments involve matching but not repeated measurements. The term repeated measures is appropriate when you made repeated measurements from each subject. It does feature "repeated measures ANOVA" which is (in the help file) said to be equivalent to random block design, but I find the explanations somewhat confusing: However, I have been asked this question by persons who work on a regular basis with GraphPad Prism. Myaov <- aov( response ~ strain + Error( experiment ), data= a ) In R, I would do this as follows, given the variables strain and experiment: a <- ame( The question is, of course, whether the strains differ. There were all in all 8 mice per experiment, and three experiments (total of 4 x 2 x 3 = 24 mice).
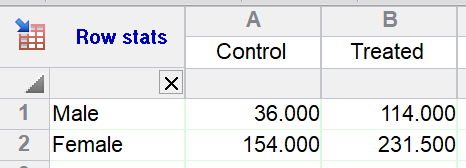
In each experiment, there were two groups corresponding to the two mouse strains compared, and each group consisted of four different mice.
Consider the following setup: two mouse strains ("KO" and "WT") have been compared in three independent experiments ("E1", "E2" and "E3").


 0 kommentar(er)
0 kommentar(er)
